Предмет: Математика,
автор: Незнайка500
Помогите пожалуйста решить, очень нужно.
Приложения:
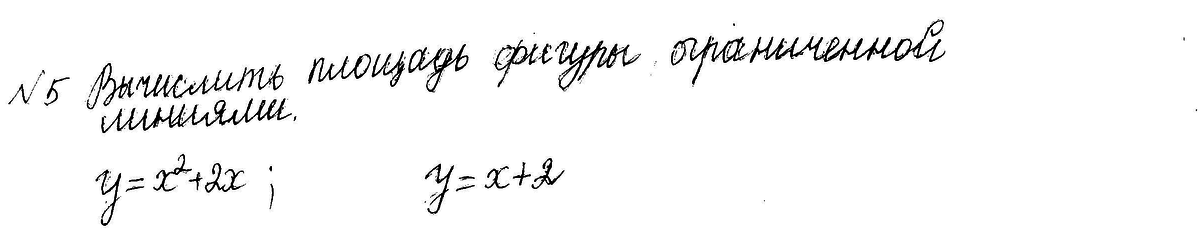
Ответы
Автор ответа:
0
Смотрим.
если схематично изобразить на графике, от очевидно, что функция линейная идет выше функции квадратичной
А точки пересечения x=-2; x=1
Тогда нам надо из интеграла линейной отнять интеграл квадратичной.
Считаем интегралы
y=x+2 F(x)=x^2/2 + 2x + c
y=x^2+2x; F(x) = x^3/3 + x^2 + C;
А дальше дело за малым.
Считаем интегралы определенные
для первой функции это 1/2+2 - (2-4)
Для второй 1/3+1 - (-8/3 + 4)
Вычитаем из первого второе. Ответ 9/2
если схематично изобразить на графике, от очевидно, что функция линейная идет выше функции квадратичной
А точки пересечения x=-2; x=1
Тогда нам надо из интеграла линейной отнять интеграл квадратичной.
Считаем интегралы
y=x+2 F(x)=x^2/2 + 2x + c
y=x^2+2x; F(x) = x^3/3 + x^2 + C;
А дальше дело за малым.
Считаем интегралы определенные
для первой функции это 1/2+2 - (2-4)
Для второй 1/3+1 - (-8/3 + 4)
Вычитаем из первого второе. Ответ 9/2
Автор ответа:
0
Найдем точки пересечения
х²+2х=х+2
х²+2х-х-2=0
х²+х-2=0
х1+х2=-1 и х1*х2=-2⇒х1=-2 и х2=1
S= =2x-x²/2-x³/3|(от -2 до 1)=
=2x-x²/2-x³/3|(от -2 до 1)=
=2-1/2-1/3+4+2-8/3=4,5
х²+2х=х+2
х²+2х-х-2=0
х²+х-2=0
х1+х2=-1 и х1*х2=-2⇒х1=-2 и х2=1
S=
=2-1/2-1/3+4+2-8/3=4,5
Интересные вопросы
Предмет: История,
автор: tusupovtimur818
Предмет: Английский язык,
автор: MAMADOVMUHAMMAD776
Предмет: Русский язык,
автор: Asel134
Предмет: Алгебра,
автор: Умнаяаня
Предмет: Физика,
автор: freeman111