Предмет: Алгебра, автор: Bernik95

Решите, пожалуйста, очень надо

Приложения:

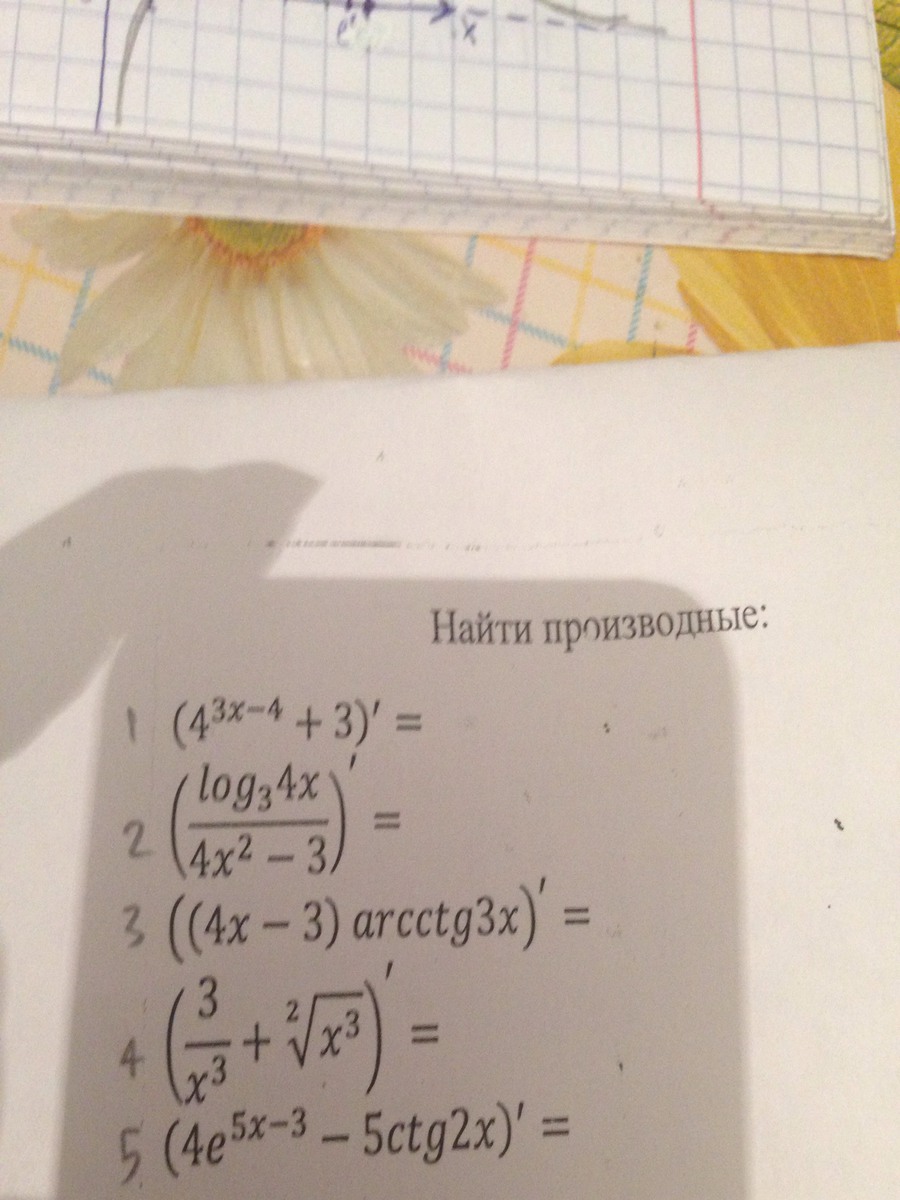
Ответы

Автор ответа: red321
0
1)
(4^{3x-4}+3)'=4^{3x-4}*ln4*(3x-4)'+0=4^{3x-4}*ln(4)*3


2)
(frac{log_34x}{4x^2-3})'=(frac{(log_34x)'*(4x^2-3)-(log_34x)*(4x^2-3)'}{(4x^2-3)^2}=\=frac{frac{1}{4x*ln3}*(4x)'-(log_34x)*8x}{(4x^2-3)^2}=frac{frac{1}{xln3}-8x(log_34x)}{(4x^2-3)^2}=frac{1-8x^2*log_3(4x)*ln3}{xln3*(4x^2-3)^2}


3)
((4x-3)*arcctg(3x))'=\=(4x-3)'*arcctg(3x)+(4x-3)*(arcctg(3x))'=\=4arcctg(3x)+(4x-3)*(-frac{1}{1+(3x)^2})*(3x)'=4acctg(3x)-frac{12x-9}{1+9x^2}


4)
(frac{3}{x^3}+sqrt[2]{x^3})'=(3x^{-3})'+(x^frac{3}{2})'=-9x^{-2}+frac{3}{2}*x^{frac{1}{2}}=-frac{9}{x^2}+frac{3sqrt{x}}{2}



5)
(4e^{5x-3}-5ctg2x)'=4*e^{5x-3}*(5x-3)'-5*(-frac{1}{sin^22x})*(2x)'=\=20e^{5x-3}+frac{10}{sin^22x}
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Химия, автор: loveyourself4com
Невозможна реакция между:
1. бромом и йодидом калия 2. бромом и хлоридом натрия 3. хлором и йодидом кальция
​
6 лет назад
Предмет: Русский язык, автор: kkylymbekov
Укажите ошибочное утверждение
1 балл
Деепричастие обозначает добавочное действие при глаголе.
В деепричастии совмещены признаки глагола и наречия.
Деепричастия бывают настоящего, прошедшего и будущего времени.
В предложении деепричастие бывает обстоятельством.
6 лет назад
Предмет: Геометрия, автор: kirkug13
40 баллов срочно нужно

Дано:

Доказать:

Доказательство:
6 лет назад
Предмет: Химия, автор: laiting
сколько молекул содержится в 1 г гелия
10 лет назад
Предмет: Физика, автор: lafleur123
ПОМОГИТЕ! утонет ли в нефти брусок размером 50х40х20 см и массой 28кг? ( плотность нефти 800кг/м кубический)
10 лет назад