Предмет: Алгебра, автор: ЛешаZn

ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ пожаалуйста!

Приложения:

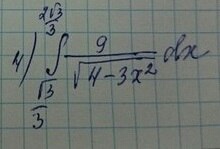
Ответы

Автор ответа: NNNLLL54

$int _{frac{sqrt3}{3}}^{frac{2sqrt3}{3}}, frac{9dx}{sqrt{4-3x^2}}=9int frac{dx}{sqrt3cdot sqrt{frac{4}{3}-x^2}}=3sqrt3int frac{dx}{sqrt{frac{4}{3}-x^2}}=3sqrt3cdot arcsinfrac{x}{frac{2}{sqrt3}}|_{frac{sqrt3}{3}}^{frac{2sqrt3}{3}}=\\=3sqrt3(arcsin1-arcsinfrac{1}{2})=3sqrt3(frac{pi}{2}-frac{pi}{6})=3sqrt3frac{pi}{3}=pi sqrt3$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Химия, автор: ahmetovakimbat1979

помагите пожалуйста срочно

6 лет назад

Предмет: Алгебра, автор: oleg89552

Решите пожалуйста 1,2 номер

6 лет назад

Предмет: История, автор: arman84091934

как назывались статьи хамураппи с 26 до 41?

6 лет назад

Предмет: Математика, автор: nik7890

периметр какой ломаной линии больше той у которой 4 звена длина каждого 3 см или той у которой 3 звена длина каждого 4см

10 лет назад

Предмет: Математика, автор: Vadimvadimnos

А1) Функция f(x) = ax(в квадрате) + bx + c задана графически. D - дискриминант соответствующего квадратного трёхчлена. Какое из высказываний верно? 1) a больше 0,D больше 0. 2) a больше 0,D меньше 0. 3) a меньше 0,D меньше 0. 4) a меньше 0,D больше 0.

А2) Решите неравенство f(x) больше или равен 0. 1) (-бесконечность;-2] U [3;бесконечность). 2) (-2;3). 3) [-2;3]. 4) (-бесконечность;4].

А3) Решите неравенство x(в квадрате) - 4x - 5 больше 0. 1) (-бесконечность;-5] U (1;бесконечность). 2) (-1;5). 3) (-5;1). 4)(-бесконечность;-1) U (5;бесконечность).

А4) Найдите множество решений неравенства (x-5)(x+3)меньше 0. 1) (-3;5). 2) (-5;3). 3) [-3;5]. 4) (-бесконечность;-3) U (5;бесконечность).

А5) Решите неравенство (5x-2)(2-x) больше или равно 0. 1) [2;2,5]. 2) [0,4;2]. 3) (-бесконечность;0,4] U [2;бесконечность). 4) (0,4;2).

А6) Найдите область определения функции f(x) = корень из 2x(в квадрате) - x -1.

1) [-одна вторая;1]. 2) (-бесконечность;-одна вторая) U (1;бесконечность). 3) (-бесконечность;-одна вторая] U [1;бесконечность). 4) (-одна вторая;1)

10 лет назад