Предмет: Геометрия, автор: Mary230999

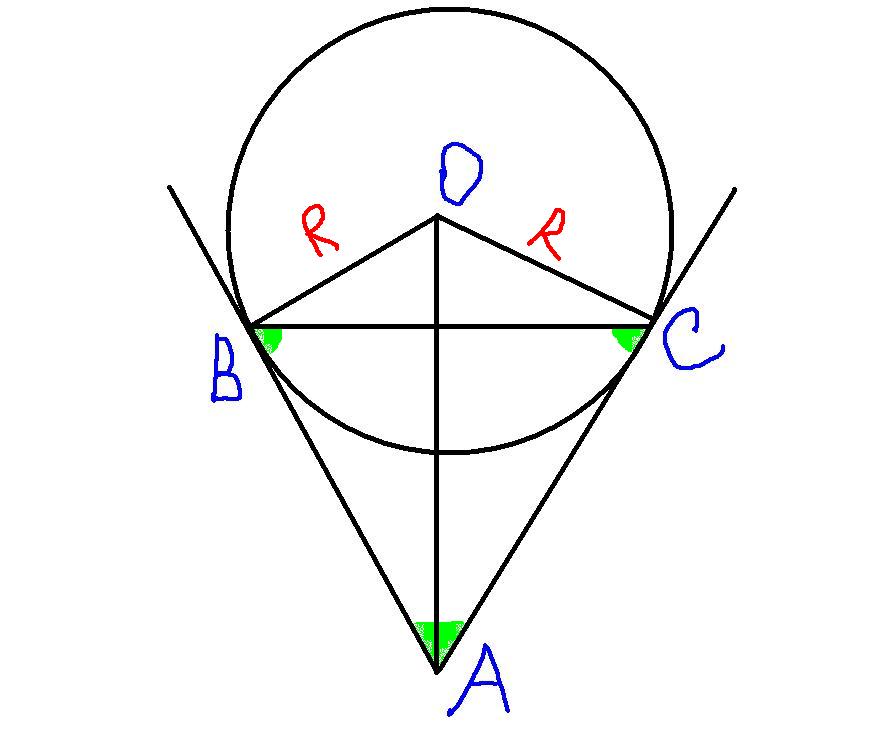
Из точки A проведены две прямые, касающиеся окружности радиуса R в точках C и B, причём треугольник ABC — равносторонний. Найдите его площадь.

Ответы

Автор ответа: Artem112

Так как треугольник АВС равносторонний, то все его углы равны по 60 градусов. Так как АВ и АС - касательные к окружности, и радиус, проведенный в точку касания перпендикулярен касательной, то углы ОВА и ОСА - прямые. Следовательно, углы СВА=ВСА=ОВА-СВА=90-60=30. Тогда, угол О=180-(2*30)=120.
По теореме косинусов находим сторону равностороннего треугольника:
$BC^2=OB^2+OC^2-2OBcdot OCcdotcos alpha \ BC^2=R^2+R^2-2R^2cos120=3R^2 \ BC=R sqrt{3}$
По формуле площади равностороннего треугольника, находим искомую площадь:
$S= frac{a^2 sqrt{3} }{4} = frac{(R sqrt{3}) ^2 sqrt{3} }{4} = frac{3R^2 sqrt{3} }{4}$
Ответ: $frac{3R^2 sqrt{3} }{4}$