Предмет: Алгебра,
автор: Danil981
Помогите решить уравнение очень надо :
Приложения:
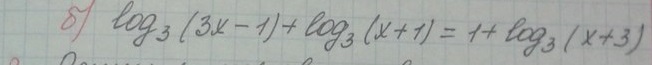
Ответы
Автор ответа:
0
Решение
log₃ (3x - 1) + log₃ (x + 1) = 1+ log₃ (x + 3)
ОДЗ: 3x - 1 > 0, x > 1/3;
x+ 1 > 0, x > - 1
x + 3 > 0, x > - 3
x ∈ (1/3; + ≈)
log₃ (3x - 1)*(x + 1) = log₃ 3 + log₃ (x + 3)
log₃ (3x - 1)*(x + 1) = log₃ (3* (x + 3))
3x² + 3x - x - 1 = 3x + 9
3x² - x - 10 = 0
D = 1 + 4*3*10 = 121
x₁ = (1 - 11)/6
x₁ = - 5/3
x₁ = - 1(2/3) не удовлетворяет ОДЗ
x₂ = (1 + 11)/6
x₂ = 2
Ответ: х = 2
log₃ (3x - 1) + log₃ (x + 1) = 1+ log₃ (x + 3)
ОДЗ: 3x - 1 > 0, x > 1/3;
x+ 1 > 0, x > - 1
x + 3 > 0, x > - 3
x ∈ (1/3; + ≈)
log₃ (3x - 1)*(x + 1) = log₃ 3 + log₃ (x + 3)
log₃ (3x - 1)*(x + 1) = log₃ (3* (x + 3))
3x² + 3x - x - 1 = 3x + 9
3x² - x - 10 = 0
D = 1 + 4*3*10 = 121
x₁ = (1 - 11)/6
x₁ = - 5/3
x₁ = - 1(2/3) не удовлетворяет ОДЗ
x₂ = (1 + 11)/6
x₂ = 2
Ответ: х = 2
Автор ответа:
0
А перед ОДЗ разве не надо ничего расписывать?
Автор ответа:
0
Можно ОДЗ записать в виде системы и всё. После ОДЗ сразу начинаем решать.
Автор ответа:
0
Можно написать словами, что логарифм нуля и отрицательных чисел не существует.
Интересные вопросы
Предмет: Химия,
автор: emmapeterson
Предмет: Литература,
автор: denisberger626
Предмет: Қазақ тiлi,
автор: aiypamyna
Предмет: Геометрия,
автор: Annyazotova
Предмет: Алгебра,
автор: vipnaqiyeva