периметр ромба,один из углов которого 120 градусов,равен 16 см.Найти диагонали ромба

P=16 см
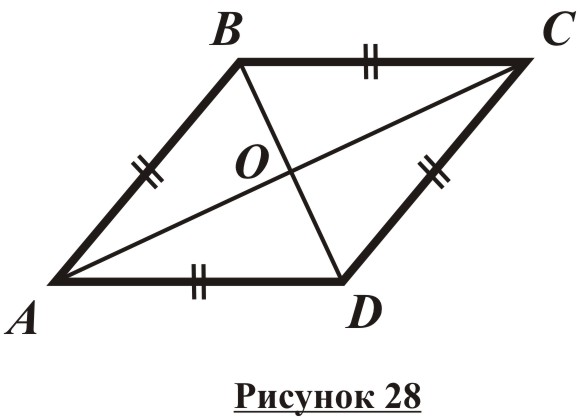
Угол ABC=120°
Т.к все стороны ромба равны, то
AB=BC=CD=DA=P/4=16/4=4 см
Угол BCD=60°(т.к (360°-120°-120°):2=60° по сумме углов четырёхугольника)
Т.к диагонали ромба являются и биссектрисами, то
Угол ABD= Угол DBC = Угол CDB = Угол BDA = 120°/2=60°
Треугольник BOC= Треугольник COD= Треугольник ODA=Треугольник OBA (по стороне и двум прилежащим к ней углам)
Рассмотрим Треугольник BOC:
Он прямоугольный, т.к диагонали ромба взаимноперпендикулярны
Т.к OC - биссектриса угла BCD, то Угол BCO=60°/2=30°
Катет, лежащий против Угла 30°, равен половине гипотенузы
BO=BC/2=4/2=2 см
Воспользуемся теоремой Пифагора
c²=a²+b²
BC²=BO²+OC²
4²=2²+OC²
OC²=16-4
OC²=12
OC=
Т.к диагонали ромба точкой пересечения делятся пополам, то
BD=2*BO=2*2=4
CA=2*CO=2*=
Ответ: Диагонали равны 4 см и  см