Предмет: Алгебра,
автор: 1vladochka1
Исследуйте функцию на монотонность и экстремумы
Приложения:
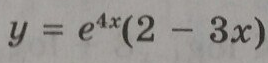
Ответы
Автор ответа:
0
Решение
1) y = (e^x)*(2 - 3x)
Найдём первую производную:
y` = (e^x)*(2 - 3x) - 3*(e^x)
Приравняем её к нулю:
(e^x)*(2 - 3x - 3) = 0
- (e^x)*(1 + 3x) = 0
3x = - 1
x = - 1/3
f(-1/3) = 3/e¹/³
Используем достаточное условие эксремума функции одной переменной.
Найдём вторую производную:
y`` = (-3x + 2)*(e^x) - 6*(e^x)
y`` = - (3x + 4)*(e^x)
y``(-1/3) = - 2,15 < 0
значит эта точка (- 1/3) - точка максимума.
2) на интервале (- ∞; - 1/3) ; f`(x) > 0 функция возрастает.
на интервале (- 1/3; + ∞) ; f`(x) < 0 функция убывает.
1) y = (e^x)*(2 - 3x)
Найдём первую производную:
y` = (e^x)*(2 - 3x) - 3*(e^x)
Приравняем её к нулю:
(e^x)*(2 - 3x - 3) = 0
- (e^x)*(1 + 3x) = 0
3x = - 1
x = - 1/3
f(-1/3) = 3/e¹/³
Используем достаточное условие эксремума функции одной переменной.
Найдём вторую производную:
y`` = (-3x + 2)*(e^x) - 6*(e^x)
y`` = - (3x + 4)*(e^x)
y``(-1/3) = - 2,15 < 0
значит эта точка (- 1/3) - точка максимума.
2) на интервале (- ∞; - 1/3) ; f`(x) > 0 функция возрастает.
на интервале (- 1/3; + ∞) ; f`(x) < 0 функция убывает.
Интересные вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: svetlana921583
Предмет: Математика,
автор: m2hdan0va37
Предмет: Математика,
автор: endzhiy
Предмет: Математика,
автор: albina20011