Предмет: Алгебра, автор: anytimes

Ребята, помогите пожалуйста

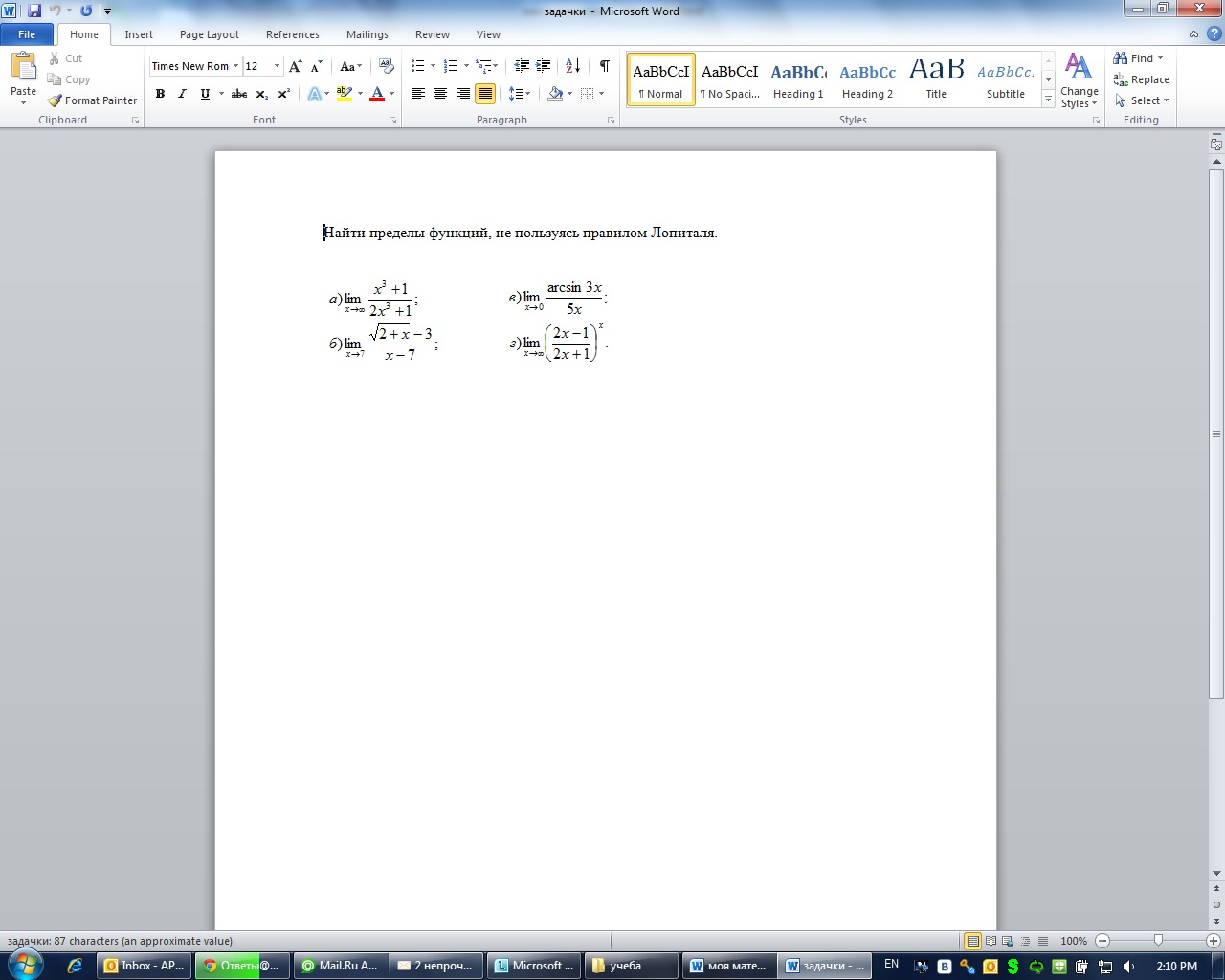
Найти пределы функций, не пользуясь правилом Лопиталя

 

Примеры во вложении...спасибо огромное зарание!!!

 

 

Приложения:

Ответы

Автор ответа: dtnth
0

lim_{x->infty} frac{x^3+1}{2x^3+1}=\\ lim_{x->infty} frac{1+frac{1}{x^3}}{2+frac{1}{x^3}}=\\ frac{1+0}{2+0}=frac{1}{2}=0.5

 

lim_{x->7} frac{sqrt{2+x}-3}{x-7}=\\ lim_{x->7} frac{sqrt{2+x}-3}{x+2-9}=\\ lim_{x->7} frac{sqrt{2+x}-3}{sqrt{x+2}-3)(sqrt{x+2}+3)}=\\ lim_{x->7} frac{1}{sqrt{x+2}+3}=\\ frac{1}{sqrt{7+2}+3}=frac{1}{6}

 

lim_{x->0} frac{arcsin (3x)}{5x}=\\ lim_{x->0} frac{arcsin (3x)}{3x}*frac{3}{5}=\\ 1*frac{3}{5}=0.6

 

 

lim_{x->infty} (frac{2x-1}{2x+2})^x=\\ lim_{t->infty} (frac{t-1}{t+2})^{frac{t}{2}}=\\ lim_{t->infty} (frac{t+2-3}{t+2})^{frac{t}{2}}=\\ lim_{t->infty} (1-frac{3}{t+2})^{frac{t}{2}}=\\ lim_{t->infty} (1+frac{1}{frac{-(t+2)}{3})}^{frac{t}{2}}=\\ lim_{t->infty} (1+frac{1}{frac{-(t+2)}{3}})}^{frac{t}{2}}=\\ lim_{u->infty} (1+frac{1}{frac{-u}{3}})}^{frac{u-2}{2}}=\\

lim_{u->infty} (1+frac{1}{frac{-u}{3}})}^{frac{u}{2}}*(1+frac{1}{frac{-u}{3}})=\\ e^{-frac{3}{2}}*1=frac{1}{e* sqrt{e}}

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Английский язык, автор: marshall18062006
СРОЧНО!!!
Вставте артикли a/an или the​
6 лет назад
Предмет: Геометрия, автор: hellokitty831
Из точки, расположенной на расстоянии 6 см от
плоскости, проведена к ней наклонная длиной
10 см. Найдите длину проекции этой наклонной.
А) 8 см
В) 3 см
C) 5 см
D) 11 см
E) 6 см
6 лет назад
Предмет: Экономика, автор: tamilaguseynowa5
12. Фирма «Минс» производит два товара. А и Б. Фирма максимально может
произвести либо 10 тысяч единиц A, либо 2,5 тысячи единиц Б, причем для
производства каякдой единицы любого из товаров нужно отказаться от
постоянного числа единиц второго товара. Товары А и Б индивиды
потребляют комплектами по одной единице А и одной единице Б. Сколько
товара в тысячах единиц произведёт и продаст фирма?
а) А = 1, Б2 1
б) А = 2,5 = 2
в) 4 = 0,5, Б = 0,5
1) A = 4, Б = 4​
6 лет назад
Предмет: Геометрия, автор: 66665

Помогите решать пжл! Только с решениями!

 

2 вариант.

1)Прямые a и b пересекаются. Прямые а и c параллельны. Могут ли прямые b и с быть скрещивающимися?

2)Плоскость альфа проходит через основание АD трапеции ABCD. Точки M и N – середины боковых сторон трапеции. а)Докажите, что MN||альфа. б) Найдите AD, если BC = 4 см, MN = 6 см.

3)Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС. а) Докажите, что CD и EF – скрещивающиеся прямые.б) Найдите угол между прямыми CD и EF, если угол DCA = 60°.
10 лет назад
Предмет: Физика, автор: саша19981998

В калориметр налили воду массой 0,39 кг при температуре 20 градусов и воду массой 0,21 кг при температуре 60 градусов.Определите установившуюся температуру воды.
10 лет назад