Предмет: Геометрия, автор: Аноним

99 баллов!!! 2 вопроса.

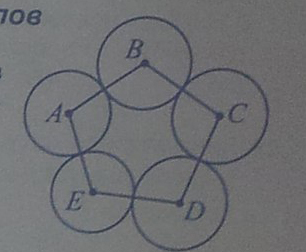
1.На рисунке изображены окружности с центрами в точках(см.рисунок).Отрезками соединены центры касающихся окружностей.Известно, что АВ=16,ВС=14,СD=17,DЕ=13,АЕ=14.В какой точке находится центр окружности наибольшего радиуса?

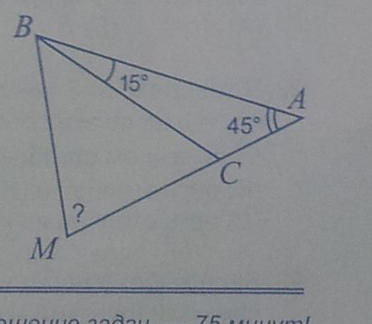
2.На продолжении стороны АС треугольника АВС отмечена точка М. Известно,что СМ=2АС,угол СВА=15 градусам, угол САВ=45 градусам. Найти угол АМВ

Приложения:

Ответы

Автор ответа: gartenzie

1.

Обозначим радиусы окружностей, соответствуюх их центрам, как:
$R_A , R_B , R_C , R_D$    и   $R_E .$

Тогда мы можем составить систему уравнений:

$left{begin{array}{l} R_A + R_B = AB , \ R_B + R_C = BC , \ R_C + R_D = CD , \ R_D + R_E = DE , \ R_E + R_A = EA ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_B + R_C = 14 , \ R_C + R_D = 17 , \ R_D + R_E = 13 , \ R_E + R_A = 14 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_B + R_C = 14 , \ R_C + R_D = 17 , \ ( R_E + R_A ) - ( R_D + R_E ) = 14 - 13 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_B + R_C = 14 , \ R_C + R_D = 17 , \ R_A - R_D = 1 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_B + R_C = 14 , \ R_C + R_D + R_A - R_D = 17+1 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_B + R_C = 14 , \ R_C + R_A = 18 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ ( R_C + R_A ) - ( R_B + R_C ) = 18 - 14 ; end{array}right$

$left{begin{array}{l} R_A + R_B = 16 , \ R_A - R_B = 4 ; end{array}right$

$R_A + R_B + R_A - R_B = 16 + 4 ;$

$2 R_A = 20 ;$

$R_A = 10 ;$

$R_B = 6 ;$

$R_C = 8 ;$

$R_D = 9 ;$

$R_E = 4 ;$

Наибольшим является радиус окружности, построенной около центра A.

О т в е т : A .

2.

Исходя из того, что в любом треугольнике сумма углов равна   $180^o ,$    легко понять, что   $angle BCA = 120^o .$

Для любого треугольника верно, что отношение любой его стороны к синусу противолежащего угла – постоянно, тогда:

[1]    $frac{AB}{ sin{ 120^o } } = frac{CB}{ sin{ 45^o } } ;$

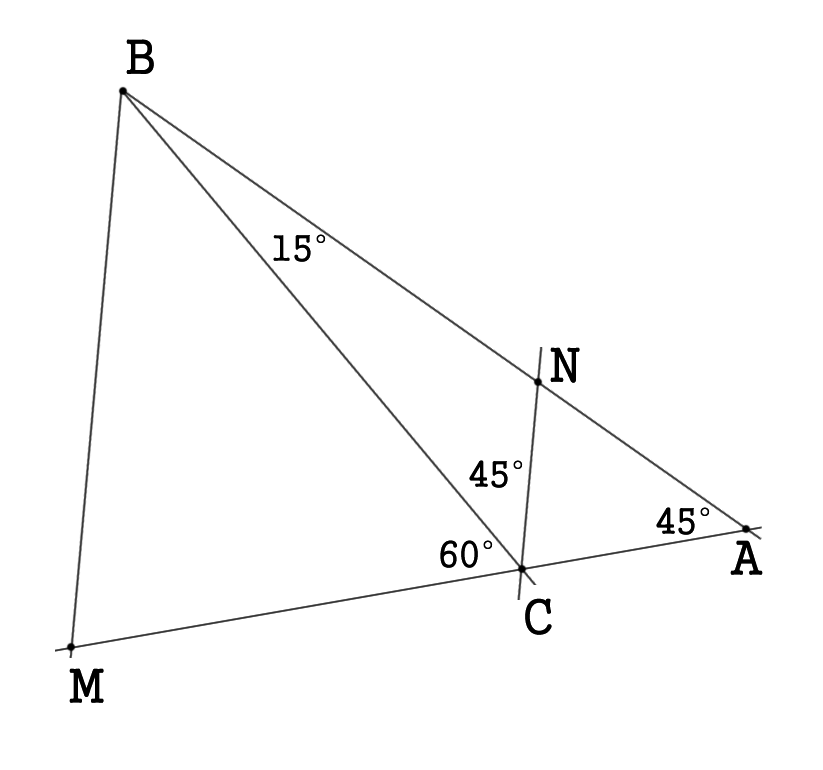
Проведём   $CN$    так, чтобы   $angle BCN = 45^o .$

Тогда   $angle CNB = 120^o .$

Опять же из соотношения синусов:

[2]    $frac{CB}{ sin{ 120^o } } = frac{NB}{ sin{ 45^o } } ;$

Перемножим выражения [1] и [2]:

$frac{AB}{ sin{ 120^o } } cdot frac{CB}{ sin{ 120^o } } = frac{CB}{ sin{ 45^o } } cdot frac{NB}{ sin{ 45^o } } ;$

$frac{AB}{ sin^2{ 120^o } } = frac{NB}{ sin^2{ 45^o } } ;$

[3]   $AB sin^2{ 45^o } = NB sin^2{ 120^o } ;$

Учитывая, что:   $sin{ 120^o } = sin{ 60^o } = frac{ sqrt{3} }{2}$    и   $sin{ 45^o } = frac{ sqrt{2} }{2} ,$    а значит:

$sin^2{ 120^o } = frac{3}{4}$    и   $sin{ 45^o } = frac{1}{2} ,$    получим из выражения [3] :

$AB cdot frac{1}{2} = NB frac{3}{4} ;$

$AB = NB frac{3}{2} ;$

$NB = frac{2}{3} AB ;$

Это как раз и позволит разрешить поставленный вопрос.

$NA = frac{1}{3} AB ;$

т.е.: NA : NB = 1 : 2 = CA : CM .

По Теореме Фалеса, пропорциональные отрезки на сторонах треугольника отсекаются параллельными прямыми, а значит:

$MB || CN ;$

$angle M = angle NCA = 180^o - 60^o - 45^o = 75^o ;$

О т в е т : $75^o .$

Приложения: