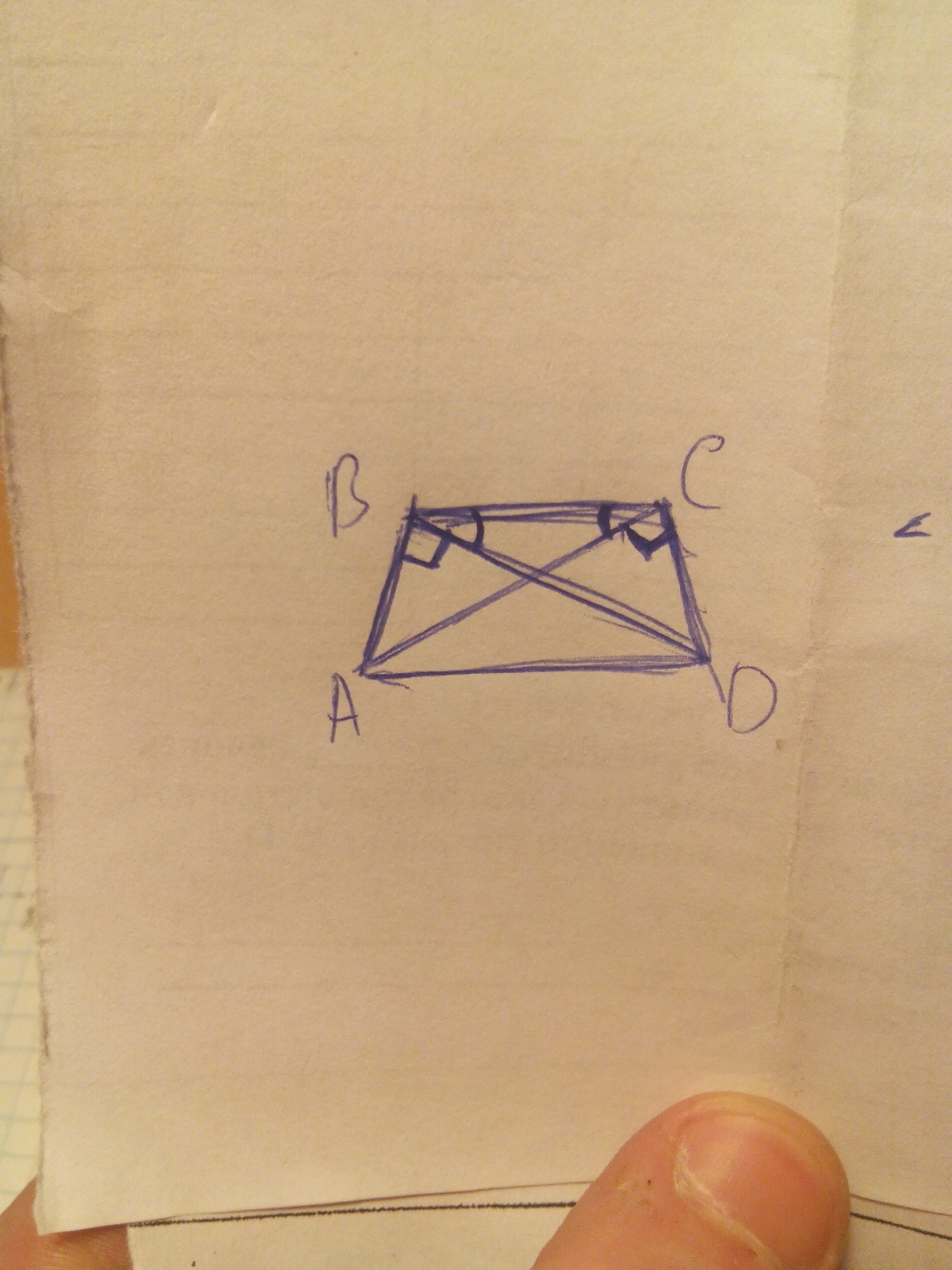
в трапеции abcd ac перпендикулярна cd,bd перпендикулярна ab, угол acb=углу cbd. доказать, что трапеция abcd равнобедренная

Обозначим точку пересечения диагоналей точкой О.
∠DBC = ∠ACB. Тогда ∆BOC - равнобедренный => BO = CO.
Рассмотрим ∆ABO и ∆DCO
BO = CO
∠ABD = ∠ACD = 90°
∠AOB =∠DOC.
Значит, ∆ABO = ∆DCO - по II признаку (или по катету и острому углу.
Из равенства треугольников => AB = CD => ABCD - равнобедренная трапеция.

уг.abc = уг.dcb т.к. уг.cbd, смежный с прям.уг.dba = уг.bca, смежному с прям.уг.acd. Из этого по св-ву трап. след., что трап. abcd - р/б.