Предмет: Алгебра,
автор: Pechenka100500
Написать к каждой формуле производной сложной функции пример с решением (образец картинка 2)
Приложения:
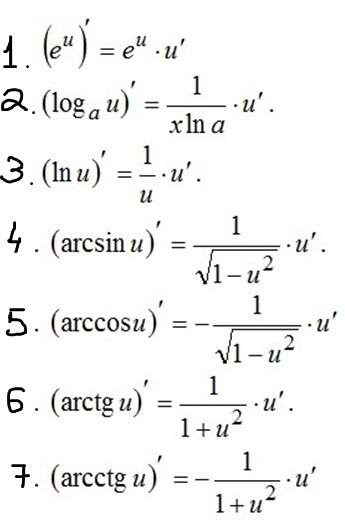
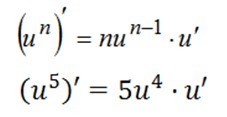
Ответы
Автор ответа:
1
1. е^(2х)=е^(2х)·(2х)'=2е^(2х).
2. log5 (x^2)=1/(x^2·ln5) ·(x^2)'= 2/(xln5).
3. ln(sinx)=1/sinx · (sinx)'= cosx/sinx = tgx.
4. arcsin(3x)= 1/корень(1-9x^2) · (3x)'. = 3/ корень(1-9х^2).
5. arccos(2x^3)=-1/ корень(1-4х^6) · (2х^3)' = -6х^2/ корень(1-4х^6).
6. arctg(e^x)= 1/(1+e^(2x) · (e^x)' = e^x/(1+e^2x).
7. arcctg(2^x)=-1/(1+2^2x) · (2^x)' = xln2 / (1 + 2^(2x))
2. log5 (x^2)=1/(x^2·ln5) ·(x^2)'= 2/(xln5).
3. ln(sinx)=1/sinx · (sinx)'= cosx/sinx = tgx.
4. arcsin(3x)= 1/корень(1-9x^2) · (3x)'. = 3/ корень(1-9х^2).
5. arccos(2x^3)=-1/ корень(1-4х^6) · (2х^3)' = -6х^2/ корень(1-4х^6).
6. arctg(e^x)= 1/(1+e^(2x) · (e^x)' = e^x/(1+e^2x).
7. arcctg(2^x)=-1/(1+2^2x) · (2^x)' = xln2 / (1 + 2^(2x))
Pechenka100500:
Хотелось бы уточнить, откуда в 7 примере появился "ln"? И разве ответ должен был получиться не отрицательным? Хм...
Не знаю в приоритете ли у Вас это, но если ответите на мои вопросы, отмечу ваш ответ как лучший.
Производная от 2 в степени х равна хln2.
Точнее, 2^х · ln2. Описочка вышла
И минус потерялся после второго равно.
Интересные вопросы
Предмет: Математика,
автор: annich000
Предмет: Математика,
автор: aierkenurgalikyzy
Предмет: Математика,
автор: jansbdvdh
Предмет: Алгебра,
автор: veseliy20
Предмет: Алгебра,
автор: dashachugay1