Предмет: Математика,
автор: B0HDAN00
Cрочно!!! Вычислить интеграл
![\int\limits^1_0 {\frac{x dx}{\sqrt[4]{(1+15x^2)^3}}}](https://tex.z-dn.net/?f=+%5Cint%5Climits%5E1_0+%7B%5Cfrac%7Bx+dx%7D%7B%5Csqrt%5B4%5D%7B%281%2B15x%5E2%29%5E3%7D%7D%7D+ "\int\limits^1_0 {\frac{x dx}{\sqrt[4]{(1+15x^2)^3}}}")
Ответы
Автор ответа:
0
Рассмотрим неопределенный интеграл:
![\int \frac{xdx}{ \sqrt[4]{(15x^2+1)^3}} = \frac{1}{30} \int \frac{d(15x^2+1)}{ \sqrt[4] {(15x^2+1)^3}} = \frac{1}{30} \int (15x^2+1)^{ -\frac{3}{4} }d(15x^2+1) =\\
= \frac{1}{30}(15x^2+1)^{ \frac{1}{4}} + C = \frac{1}{30} \sqrt[4]{15x^2+1}} + C](https://tex.z-dn.net/?f=%5Cint++%5Cfrac%7Bxdx%7D%7B+%5Csqrt%5B4%5D%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D+%5Cfrac%7B1%7D%7B30%7D+%5Cint++%5Cfrac%7Bd%2815x%5E2%2B1%29%7D%7B+%5Csqrt%5B4%5D+%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D++%5Cfrac%7B1%7D%7B30%7D+%5Cint+%2815x%5E2%2B1%29%5E%7B+-%5Cfrac%7B3%7D%7B4%7D+%7Dd%2815x%5E2%2B1%29+%3D%5C%5C%0A%3D+%5Cfrac%7B1%7D%7B30%7D%2815x%5E2%2B1%29%5E%7B+%5Cfrac%7B1%7D%7B4%7D%7D+%2B+C+%3D+%5Cfrac%7B1%7D%7B30%7D+%5Csqrt%5B4%5D%7B15x%5E2%2B1%7D%7D+%2B+C "\int \frac{xdx}{ \sqrt[4]{(15x^2+1)^3}} = \frac{1}{30} \int \frac{d(15x^2+1)}{ \sqrt[4] {(15x^2+1)^3}} = \frac{1}{30} \int (15x^2+1)^{ -\frac{3}{4} }d(15x^2+1) =\\
= \frac{1}{30}(15x^2+1)^{ \frac{1}{4}} + C = \frac{1}{30} \sqrt[4]{15x^2+1}} + C")
Используем пределы интегрирования:
![\int \limits_{0}^{1} \frac{xdx}{ \sqrt[4]{(15x^2+1)^3}} = \frac{1}{30} \sqrt[4]{15x^2+1}} \big | _{0}^{1} = \frac{1}{30}\sqrt[4]{15+1}- \frac{1}{30}\sqrt[4]{0+1}=\\
=\frac{1}{30}*2-\frac{1}{30} = \frac{1}{30}.](https://tex.z-dn.net/?f=%5Cint+%5Climits_%7B0%7D%5E%7B1%7D+%5Cfrac%7Bxdx%7D%7B+%5Csqrt%5B4%5D%7B%2815x%5E2%2B1%29%5E3%7D%7D+%3D+%5Cfrac%7B1%7D%7B30%7D+%5Csqrt%5B4%5D%7B15x%5E2%2B1%7D%7D+%5Cbig+%7C+_%7B0%7D%5E%7B1%7D++%3D++%5Cfrac%7B1%7D%7B30%7D%5Csqrt%5B4%5D%7B15%2B1%7D-+%5Cfrac%7B1%7D%7B30%7D%5Csqrt%5B4%5D%7B0%2B1%7D%3D%5C%5C%0A%3D%5Cfrac%7B1%7D%7B30%7D%2A2-%5Cfrac%7B1%7D%7B30%7D+%3D+%5Cfrac%7B1%7D%7B30%7D. "\int \limits_{0}^{1} \frac{xdx}{ \sqrt[4]{(15x^2+1)^3}} = \frac{1}{30} \sqrt[4]{15x^2+1}} \big | _{0}^{1} = \frac{1}{30}\sqrt[4]{15+1}- \frac{1}{30}\sqrt[4]{0+1}=\\
=\frac{1}{30}*2-\frac{1}{30} = \frac{1}{30}.")
Используем пределы интегрирования:
Приложения:
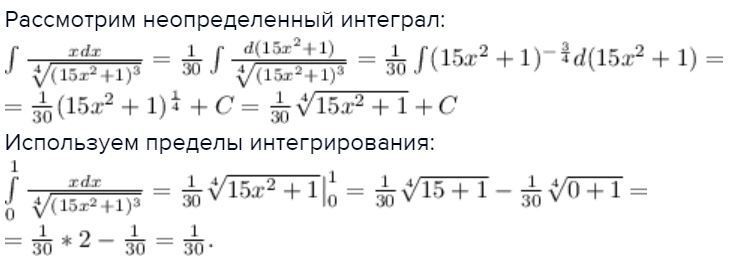
Интересные вопросы
Предмет: История,
автор: anastasianazarcuk764
Предмет: Английский язык,
автор: polinamilota11
Предмет: История,
автор: Natr1Xx
Предмет: Математика,
автор: ольга638
Предмет: Алгебра,
автор: asdfghjkl48