Предмет: Математика, автор: Nastya171167

нужно найти производные функций

Приложения:

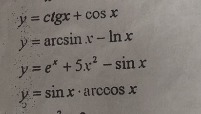
Nastya171167: понятно мне нужно полное решение

Ответы

Автор ответа: rina2403k

$y = \cot(x) + \cos(x) \\ \frac{d}{dx} = ( \cot(x) ) + \frac{d}{dx} ( \cos(x) ) \\ - \cos(x) {}^{2} - \sin(x) \\ - \frac{1 + \sin(x) {}^{3} }{ \sin(x) {}^{2} } \\ y = arc \sin(x) - ln(x) \\ \frac{d}{dx} (arc \sin(x) ) - \frac{d}{dx} ( ln(x) ) \\ \frac{1}{ \sqrt{1 - x {}^{2} } } - \frac{1}{x} \\ y = e {}^{x} + 5x {}^{2} - \sin(x) \\ \frac{d}{dx} (e {}^{x} ) + \frac{d}{dx} (5x {}^{2} ) - \frac{d}{dx} ( \sin(x) ) \\ e {}^{x} + 5 \times 2x - \cos(x) \\ e {}^{x} + 10x - \cos(x) \\ y = \sin(x) \times arc \cos(x) \\ \frac{d}{dx} ( \sin(x) ) \times (arc \cos(x) ) + \sin(x) \times \frac{d}{dx} (arc \cos(x) ) \\ \cos(x) arc \cos(x) + \sin(x) \times ( - \frac{1}{ \sqrt{1 - x {}^{2} } } ) \\ \cos(x) \times arc \cos(x) - \frac{ \sin(x) }{ \sqrt{1 - x {}^{2} } }$

Автор ответа: IrkaShevko

Ответ:

Пошаговое объяснение:

$y' = -\frac{1}{sin^2x} -sinx\\\\y'=\frac{1}{\sqrt{1-x^2} } -\frac{1}{x} \\\\y'=e^x+10x-cosx\\\\y'=cosx*arccosx-\frac{sinx}{\sqrt{1-x^2} }$

формулы (табличные значения):

$(sinx)' = cosx\\\\(cosx)' = -sinx\\\\(arcsinx)'=\frac{1}{\sqrt{1-x^2} } \\\\(arccosx)'=-\frac{1}{\sqrt{1-x^2} } \\\\(ctgx)'=-\frac{1}{sin^2x}\\\\ (lnx)'=\frac{1}{x} \\\\(e^x)'=e^x\\\\(x^n)'=nx^{n-1}\\\\(u*v)'=u'*v+u*v'$