Предмет: Математика, автор: Элитный

Помогите с пределами, возможно вы измените мою жизнь и научите хоть чему то!

Приложения:

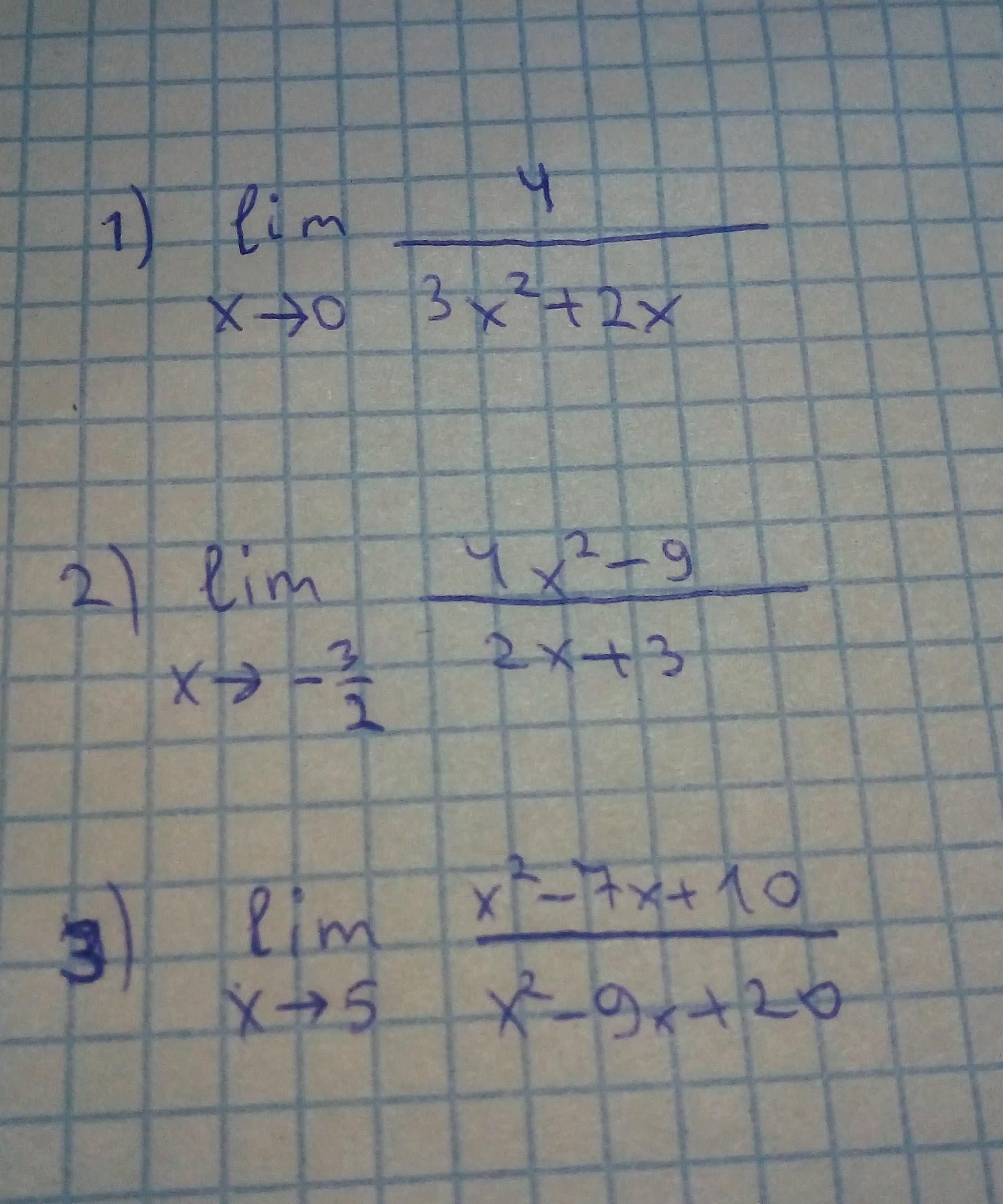
Ответы

Автор ответа: Tanda80

$\lim\limits _{x \to0} \frac{4}{3 {x}^{2} + 2x} = \frac{4}{0} = \infty$

$\lim\limits _{x \to - \frac{3}{2} } \frac{4 {x}^{2} - 9 }{2x + 3} = ( \frac{0}{0} ) = \\ = \lim\limits _{x \to - \frac{3}{2} } \frac{(2x - 3)(2x + 3)}{2x + 3} = \\ = \lim\limits _{x \to - \frac{3}{2} }(2x - 3) = \\ = 2 \times ( - \frac{3}{2} ) - 3 = - 6$

$\lim\limits _{x \to5} \frac{ {x}^{2} - 7x + 10 }{ {x}^{2} - 9x + 20 } = ( \frac{0}{0} ) = \\ = \lim\limits _{x \to5} \frac{(x - 5)(x - 2)}{(x - 5)(x - 4)} = \\ = \lim\limits _{x \to5} \frac{x - 2}{x - 4} = \frac{5 - 2}{5 - 4} = 3$

Элитный: А почему в последнем примере (х-5)(х-2) если корни х это +5 и +2, ведь корни находятся по формуле -b+-√x/2*число перед х^2

Tanda80: Потому что квадратный трехчлен раскладывается на множители по формуле а*х^2+b*x+c=a(x-x1)(x-x2), где х1 и х2 - корни квадратного уравнения

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Геометрия, автор: adriatutunnik

у трикутнику ABC відомо що c=90 AC=8см. BC=6см знайдіть sin кута A cos кута A tg кута B ctg кута B

5 лет назад

Предмет: Информатика, автор: safina10082008

Объясните питон 7 класс, пожалуйста

5 лет назад

Предмет: Алгебра, автор: darinasumilo