Помогите пожалуйста с геометрией. ​

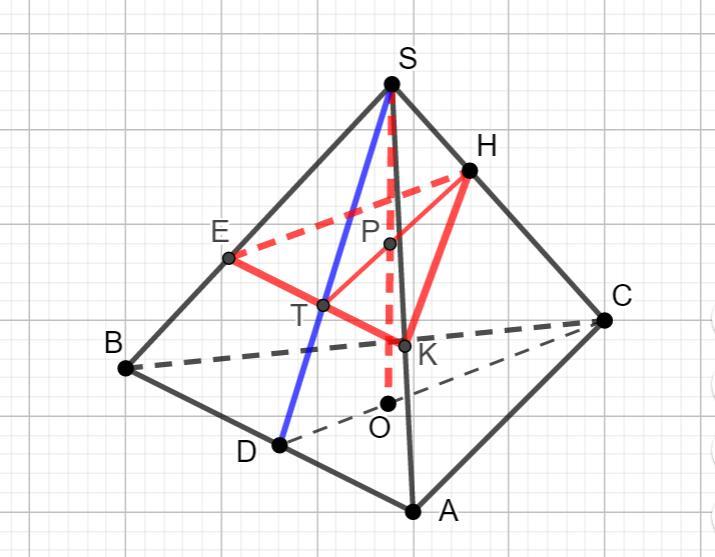
Проведём осевое сечение пирамиды перпендикулярно ребру основания. Получит равнобедренный треугольник CDS.

DS = CD = 6*cos 30° = 6*√3/2 = 3√3.

По свойству правильной пирамиды вершина S проецируется на основание в точку О. DO = (1/3)DC = (1/3)*6*(√3/2) = √3.

OC = 2DO = 2√3.

Высота пирамиды Н = √(6² - DO²) = √(36 - 12) = √24 = 2√6.

По условию задания точка P делит высоту пополам, значит, SP = √6.

Из подобия треугольников SH/PS = OS/SC.

Отсюда SН = PS*OS/CS = √6*2√6/6 = 2.

Угол DSC = DCS.  

cos(DSC) = 2√3/6 = √3/3.

Находим отрезок ST:

ST = SH/cos(DSC) = 2/(√3/3) = 6/√3 = 2√3.

Рассмотрим грань ASB. Треугольники ASB и ESK  подобны с коэффициентом к = SD / ST = (3√3)/(2√3) = 3/2.

Отсюда длина ЕК равна:

ЕК = АВ/(3/2) = 6*2/3 = 4.

Находим высоту сечения:

ТН = √((2√3)² - 2²) = √(12 - 4) = √8 = 2√2.

Ответ: S(EKH) = (1/2)*4*(2√2) = 4√2.