Предмет: Геометрия,
автор: СамСебе
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четывре раза больше площади треугольника BOC.
Ответы
Автор ответа:
0
Вспомните, что диагонали параллелограмма точкой пересечения делятся пополам. Площади обраовавшихся треугольников равны. См. вложение
Приложения:
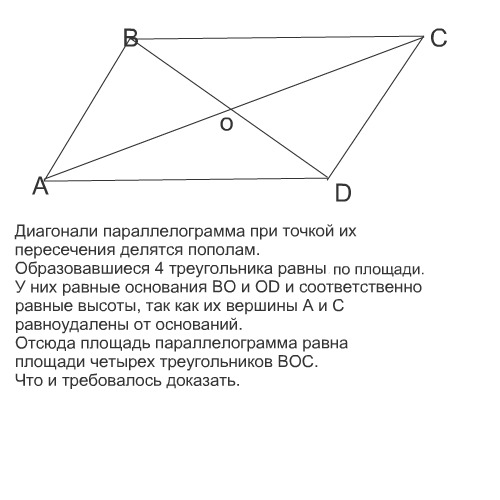
Автор ответа:
0
Диагонали параллелограмма делятся при пересечении пополам.
Без проблем можно доказать, что тр-к АВО = тр-ку СОD, а тр-к ВОС=тр-ку АОD по двум сторонам и углу между ними. Рассмотрим тр-к АОВ и ВОС, площадь тр-ка равна половине произведения основания на высоту. Основания этих тр-ков равны, а высота общая. Значит их площади равны. Из выше сказанного следует, что площади всех четырех труугольников равны между собой. Т.е. площадь параллелограмма в 4 раза больше площади тр-ка.
Приложения:

Интересные вопросы
Предмет: Математика,
автор: makosaomg
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: muhanovalihan4
Предмет: Математика,
автор: Аноним