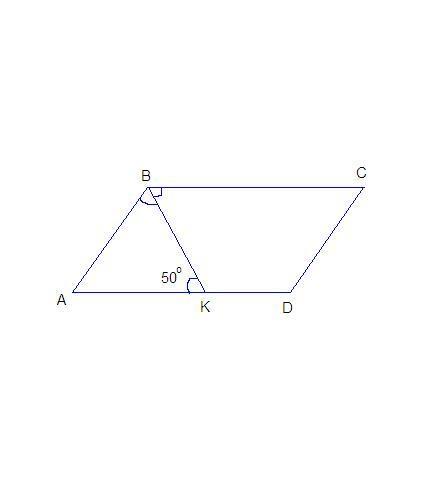
В параллелограмме ABCD луч BK - биссектриса угла ABC. Найдите углы параллелограмма ABCD, если угол BKA = 50 градусам.

∠CBK = ∠BKA = 50° как накрест лежащие при пересечении AD║BC секущей ВК.
∠АВК = ∠СВК = 50°, т.к. ВК биссектриса.
⇒ ∠АВС = 50° · 2 = 100°
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
∠ВАD = 180° - ∠АВС = 180° - 100° = 80°
В параллелограмме противолежащие углы равны.
Ответ: ∠А = ∠С = 80°, ∠В = ∠D = 100°