Предмет: Математика,
автор: annie97horan
Помогите с решением,задание во вложениях)
Приложения:
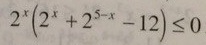
Ответы
Автор ответа:
1
Решим задание методом интервалов.
2^x не влияет на наше неравенство, так как при любом x 2^x больше 0.
Остаётся решить неравенство:

Пусть
Тогда:

Так как наше неравенство меньше 0, берём внутренний промежуток:

Вернёмся к замене:
![2^x \geq 4 \\ 2^x \leq 8
\\ \\ x \geq 2 \\
x \leq 3
\\
x \in [2;3] 2^x \geq 4 \\ 2^x \leq 8
\\ \\ x \geq 2 \\
x \leq 3
\\
x \in [2;3]](https://tex.z-dn.net/?f=2%5Ex++%5Cgeq+4+%5C%5C+2%5Ex++%5Cleq+8%0A+%5C%5C++%5C%5C+x++%5Cgeq+2+%5C%5C+%0Ax+%5Cleq++3%0A+%5C%5C+%0Ax+%5Cin+%5B2%3B3%5D)
2^x не влияет на наше неравенство, так как при любом x 2^x больше 0.
Остаётся решить неравенство:
Пусть
Тогда:
Так как наше неравенство меньше 0, берём внутренний промежуток:
Вернёмся к замене:
Автор ответа:
1
Выражение 2^(5-x) равносильно 2^5 / 2^x. Заменим 2^x = y
Выражение в скобках и всё выражение приводим к общему знаменателю: y²(y²-12y+32)≤0
Отсюда первое решение: y₁ ≤ 0, но его отбрасываем, так как 2^x не может быть равно 0 или отрицательным по свойству степеней.
Выражение в скобках приравняем нулю:
y²-12y+32 = 0.
Квадратное уравнение, решаем относительно y:
Ищем дискриминант:D=(-12)^2-4*1*32=144-4*32=144-128=16;
Дискриминант больше 0, уравнение имеет 2 корня:
y₁=(√16-(-12))/(2*1)=(4-(-12))/2=(4+12)/2=16/2=8;
y₂=(-√16-(-12))/(2*1)=(-4-(-12))/2=(-4+12)/2=8/2=4.
Возвращаем исходную неизвестную:
2^x = 8 = 2³
x₁ = 3
2^x = 4 = 2²
x₂ = 2.
Для выбора области значений, удовлетворяющих заданию, находим значения функции вблизи найденных точек:
2⁴(2⁴+2^(5-4)-12) = 16(16+2-12) = 96 - это больше 0.
Аналогично решаем левее точки 2.
Ответ 2 ≤ x ≤ 3.
Выражение в скобках и всё выражение приводим к общему знаменателю: y²(y²-12y+32)≤0
Отсюда первое решение: y₁ ≤ 0, но его отбрасываем, так как 2^x не может быть равно 0 или отрицательным по свойству степеней.
Выражение в скобках приравняем нулю:
y²-12y+32 = 0.
Квадратное уравнение, решаем относительно y:
Ищем дискриминант:D=(-12)^2-4*1*32=144-4*32=144-128=16;
Дискриминант больше 0, уравнение имеет 2 корня:
y₁=(√16-(-12))/(2*1)=(4-(-12))/2=(4+12)/2=16/2=8;
y₂=(-√16-(-12))/(2*1)=(-4-(-12))/2=(-4+12)/2=8/2=4.
Возвращаем исходную неизвестную:
2^x = 8 = 2³
x₁ = 3
2^x = 4 = 2²
x₂ = 2.
Для выбора области значений, удовлетворяющих заданию, находим значения функции вблизи найденных точек:
2⁴(2⁴+2^(5-4)-12) = 16(16+2-12) = 96 - это больше 0.
Аналогично решаем левее точки 2.
Ответ 2 ≤ x ≤ 3.
Интересные вопросы
Предмет: Русский язык,
автор: msabdi
Предмет: Русский язык,
автор: Амина77197
Предмет: Русский язык,
автор: DnevnikWolka
Предмет: Физика,
автор: lam855